Hệ số tương quan (Correlation) – Khái niệm và Ứng dụng
1. Hệ số tương quan là gì?
Hệ số tương quan (Correlation coefficient) đo lường mức độ và hướng của mối quan hệ giữa hai biến số. Nó giúp xác định xem hai biến có xu hướng di chuyển cùng chiều, ngược chiều hay không có mối quan hệ rõ ràng với nhau.
Hệ số tương quan thường được ký hiệu là r (nếu là hệ số tương quan Pearson) hoặc ρ (nếu xét trên tổng thể). Giá trị của hệ số tương quan nằm trong khoảng từ -1 đến 1, cụ thể:
- r = 1: Hai biến có tương quan dương hoàn hảo – khi một biến tăng, biến kia cũng tăng theo tỷ lệ tương ứng.
- r = -1: Hai biến có tương quan âm hoàn hảo – khi một biến tăng, biến kia giảm theo tỷ lệ tương ứng.
- r = 0: Hai biến không có mối quan hệ tương quan.
2. Các loại hệ số tương quan
Có nhiều cách đo lường tương quan giữa hai biến, phổ biến nhất gồm:
a) Hệ số tương quan Pearson
Hệ số tương quan Pearson đo lường mối quan hệ tuyến tính giữa hai biến số, được tính theo công thức:

Trong đó:

Hệ số này chỉ có ý nghĩa khi mối quan hệ giữa hai biến là tuyến tính.
b) Hệ số tương quan Spearman
Hệ số tương quan Spearman đo mối quan hệ giữa hai biến dựa trên thứ hạng của chúng, phù hợp với dữ liệu không tuyến tính. Công thức của Spearman là:
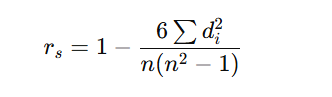
Trong đó:
- d(i) là sự khác biệt giữa thứ hạng của hai biến tại từng quan sát
- n là số quan sát
c) Hệ số tương quan Kendall
Hệ số này đo lường mối quan hệ giữa hai biến dựa trên số lượng cặp quan sát có thứ tự tương đối giống nhau hoặc khác nhau.
3. Ứng dụng của hệ số tương quan
- Tài chính – Đầu tư: Đánh giá mức độ liên quan giữa hai loại tài sản (cổ phiếu, trái phiếu, vàng…) để tối ưu hóa danh mục đầu tư.
- Kinh tế học: Phân tích mối quan hệ giữa các biến số kinh tế như lạm phát và lãi suất.
- Khoa học dữ liệu – Machine Learning: Kiểm tra mức độ phụ thuộc giữa các biến đầu vào trước khi xây dựng mô hình dự báo.
- Y học & Khoa học xã hội: Đo lường mức độ liên quan giữa hai nhân tố trong nghiên cứu (ví dụ: mối quan hệ giữa mức độ tập thể dục và huyết áp).
4. Hạn chế của hệ số tương quan
- Không thể xác định quan hệ nhân quả, chỉ thể hiện mức độ liên quan.
- Nhạy cảm với dữ liệu ngoại lai (outliers).
- Không phản ánh được các mối quan hệ phi tuyến tính.
Hệ số tương quan là công cụ mạnh mẽ để phân tích dữ liệu nhưng cần kết hợp với các phương pháp khác để có đánh giá chính xác hơn.
Hãy comment, like bài viết nếu thấy hay ho nhé !